题解 - Luogu P4055 [JSOI2009]游戏

题意

在一个格点图上，两方轮流移动棋子一步，不能移到已走过的位置，移不动者输。问如何设定棋子的初始位置，使得后手必胜？

分析

将这题可以分类为一类 二分图博弈 问题。

为什么是二分图？

这是一个常用的转换技巧，在许多网络流题目中体现的更精湛。一般一个网格图按照国际象棋的染色方式，可以被染成一个二分图。

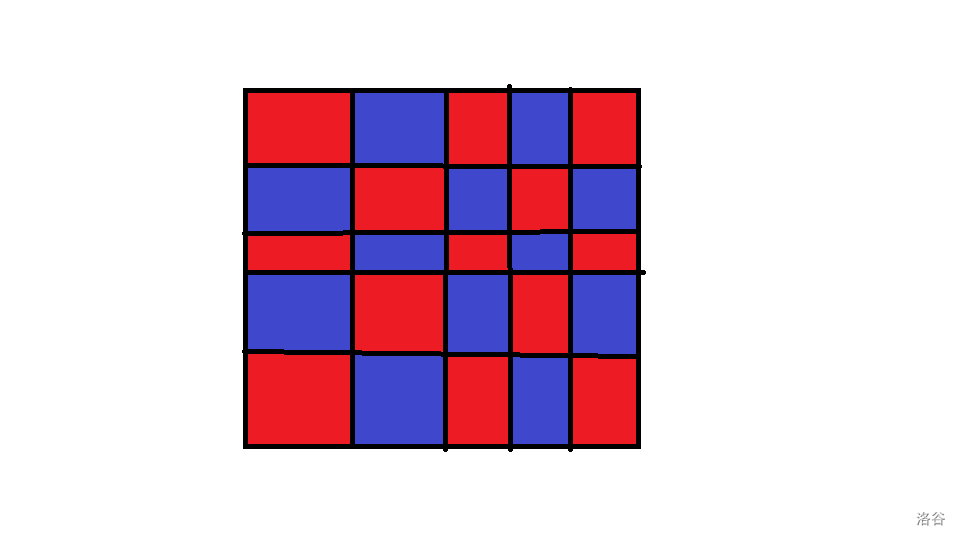
对于点 $(x,y)$，颜色就是 $x+y$ 的奇偶。

转换后要怎么做？

首先给出一个大家都知道的结论：在这个博弈中，如果初始在二分图的所有最大匹配上，那么先手必胜，反之后手必胜。

为什么我是对的？

先给出样例的拟图：

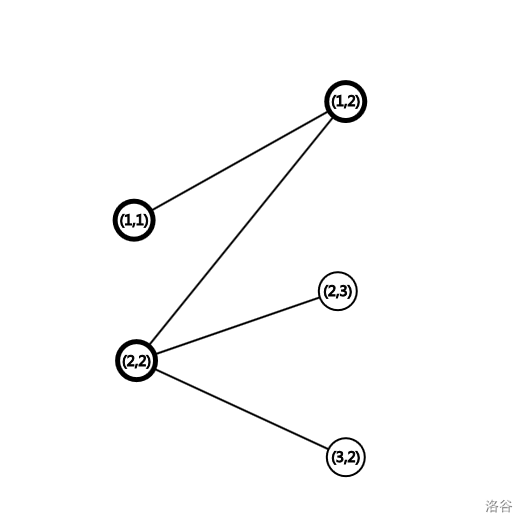
其中加粗的点为在任意最大匹配上的点。不妨先称为“粗点”，相对地有“细点”。

可以发现，从一个粗点出发（如 $(2,2)$），只需要任意选择一个在任意一个最大匹配上的匹配点（$(2,3)$ 或 $(3,2)$）即可。只要先手走的是最大匹配，无论后手怎么走，因为题目要求不能回头，所以一定可以继续沿着一个最大匹配走。

梳理一下这是怎么回事：只要先手在粗点，那么无论对方怎么走，永远可以再次走最大匹配。如果不可以，这就与最大匹配的“最大”矛盾了。

反之，如果在细点上，那么后手一定可以在一个粗点上出发，即后手必胜。

所以，题目所求的就转化为：求在一个二分图上，有哪些点不一定在最大匹配上。

只要求出这个细点集，空（也就是说，存在完美匹配，任意点皆为粗点）即输出 LOSE，非空输出 WIN 即可。

具体地怎么实现？

首先用任意可以解决二分图最大匹配问题的算法（匈牙利或 Dinic）都可以。此时我们知道，不在当前匹配的点必然是细点。

接下去，我们可以做一个 DFS。如果一个点 $P$ 已被证实是细点，设它有一边连着 $Q$，且 $Q$ 在最大匹配上，则 $Q$ 的匹配点也是细点。如样例，如果当前 $(2,2)$ 匹配 $(2,3)$，当我们从 $(3,2)$ 开始 DFS 时，就会发现 $(2,3)$ 是细点。想想看，将 $(2,2)\Rightarrow(2,3)$ 换成 $(2,2)\Rightarrow(3,2)$ 都是最大匹配。根据这样的性质，找出所有的细点即可。

主要代码

constexpr int MXN = 101;
constexpr int MXPTS = 10001;

bool enable[MXPTS];
int n, m, pts;

inline int id(int x, int y) { return x * m + y; }

int head[MXPTS], to[MXPTS << 2], nxt[MXPTS << 2], es;  // for base graph
int link[MXPTS], vis[MXPTS];                           // for bi-graph
void init() {
  fill(head, head + pts, -1);
  fill(link, link + pts, -1);
  fill(vis, vis + pts, -1);
}
void addedge(int f, int t) {
  to[es] = t;
  nxt[es] = head[f];
  head[f] = es++;
}
bool ask(int cur, int t) {
  if (vis[cur] == t) return false;
  vis[cur] = t;
  for (int i(head[cur]); ~i; i = nxt[i]) {
    if (!~link[to[i]] || ask(link[to[i]], t)) {
      link[to[i]] = cur;
      return true;
    }
  }
  return false;
}
void makepair() {
  for (int i(0); i != n; ++i) {
    for (int j(0); j != m; ++j) {
      if (!((i + j) & 1) && enable[id(i, j)]) ask(id(i, j), id(i, j));
    }
  }
  for (int i(0); i != pts; ++i) {
    if (~link[i]) link[link[i]] = i;
  }
}

bool cango[MXPTS], ans;

void findfake(int cur) {
  ans = cango[cur] = true;
  for (int i(head[cur]); ~i; i = nxt[i]) {
    if (~link[to[i]] && !cango[link[to[i]]]) findfake(link[to[i]]);
  }
}

int main() {
  cin >> n >> m;
  pts = n * m;
  init();
  for (int i(0); i != pts; ++i) {
    char c;
    cin >> c;
    if (c == '.') enable[i] = true;
  }
  for (int i(0); i != n; ++i) {
    for (int j(0); j != m; ++j) {
      if (enable[id(i, j)]) {
        if (i != n - 1 && enable[id(i + 1, j)])
          addedge(id(i, j), id(i + 1, j)), addedge(id(i + 1, j), id(i, j));
        if (j != m - 1 && enable[id(i, j + 1)])
          addedge(id(i, j), id(i, j + 1)), addedge(id(i, j + 1), id(i, j));
      }
    }
  }
  makepair();
  for (int i(0); i != pts; ++i) {
    if (enable[i] && !~link[i]) {
      findfake(i);
    }
  }
  puts(ans ? "WIN" : "LOSE");
  for (int i(0); i != n; ++i) {
    for (int j(0); j != m; ++j) {
      if (cango[id(i, j)]) cout << i + 1 << ' ' << j + 1 << endl;
    }
  }
  return 0;
}