题解 - ARC210D Independent Set Game
更少的结论,更多的分析。我看搓 D 题还是难于直接爆 E 的。
简述题意
给定一 点 边无向图,A 和 B 两人轮流行动(A 先手):
- A 选择一个没涂色的点,涂黑;
- B 选择一个没涂色的点,涂白。
A 获胜当且仅当黑点是独立集。判断最优策略下游戏的胜负。。
约定和简单转化
可以理解为 A 每次必须删掉一个点的 1-邻域,B 每次可以删掉一个点,A 获胜当且仅当他可以执行 次操作。
下文令 表示 个点的链,没有特别说明的时候默认指代一个极大连通块,孤点指的就是一个极大连通块同时是 。 表示 点的度数。
点数是奇数
A 是最后一个操作的人,发现 A 每次必须恰好删除一个点,要不然 B 只需要每次删掉某个没删过的点,A 就倒闭了。
只要场上有孤点,A 一定会抢,所以 B 为了让 A 无法操作,他也一定会抢。
- 孤点有偶数个;轮流拿完之后 A 没有孤点拿,必败;
- 孤点有奇数个:轮流拿完之后 B 选择一个点拿走,只要不产生新的孤点 A 就输了,所以 A 胜等价于剩余连通块都是 。
总结一下: 是奇数的时候,A 获胜当且仅当图中只有 或 。
我们称这样的图是破碎的。
点数是偶数
B 是最后一个操作的人,A 至多允许有一步操作恰好删了两个点,那就必须是一个一度点和这个点的邻点,我们称这样的操作为奇异操作,下文用 分别代称一度点和其邻点。如果图不是破碎的,那么 A 一定会做奇异操作。
同上的,如果有孤点,双方一定会抢。
孤点有偶数个
抢完孤点,现在剩余点数为偶,轮到 A 走,他只能走奇异操作。
这之后轮到 B 走,B 的策略仍然是先抢孤点,只要某个时刻场上没有孤点,且存在非 的连通块,B 就可以在这个连通块上找一个非割点删去,然后 A 就必然失败了。
所以 A 奇异操作胜利的条件是操作后图是破碎的。换言之,所有 子图都必须经过 或 ,显然这里只提及 也是对的。
刻画一下图的形态,除去所有的 ,图大概长得像:
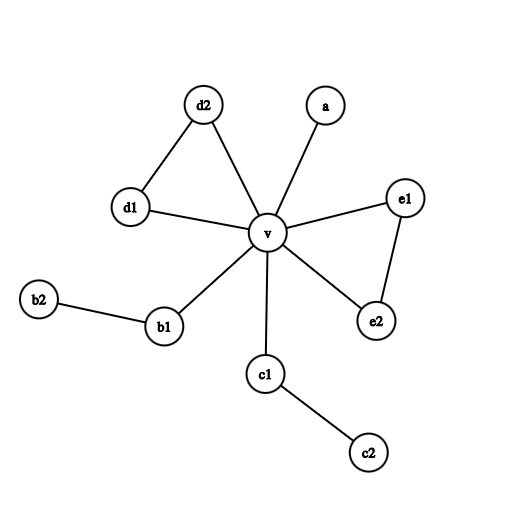
总之就是,应该是有一些 接在 上面,接了 条边。
时,。 不可能,因为 有一度点作为邻点而 所在的连通块不是 。
因此我们任选一个度数最大的点作为 ,删掉 然后检查图是否破碎然后模拟即可。即可。
关于不用考虑 的说明:如果 A 胜,由于所有拉出去的 和三元环,除去 以外剩下的两个点可以匹配,而总点数为偶,所以一定剩余至少一个和 相邻的一度点,随便拿一个作为 都没有关系。而且,不找这个 也不会影响正确性。
总结一下:此时奇异操作已经被确定,令 为度数最大的点,删去 ,判剩余的图是不是破碎的即可。
孤点有奇数个
抢完孤点,现在剩余点数为奇,轮到 B 走。A 必胜的条件是:无论 B 这一步删哪个点(下文称其为 ),A 都有一个能赢的奇异操作。
问题就在于:B 的操作,可能改变场上度数最大的点。
我们先约定 B 不会删一个 里的点,这毫无意义。
……我们还有一点性质没用。
B 的操作对 的影响不超过 ,所以如果存在 ,合法的 仍然不超过一个( 是必须被 A 删掉的,所以 的选择会节省 A 的奇异操作,对 B 不优)。
然后就变成要判断剩下的图里,无论选什么 ,都不会存在 ,也就是说剩下的图是破碎的。考虑删完 剩下的图点数得是偶数了,所以剩下的图刚好是一个 其实是无理的。
解决了这个情形,然后就是 。然后 只能从度数为 的点里面选,我们称这些点是好点,有 个。 的时候 是唯一确定的,接下来讨论 。
记 表示点 的 1-邻域里好点的个数,如果存在 ,那么令 ,剩下的备选好点就至少有 ,倒闭了。
否则
又由于
考虑现在还有 个点时,得
时 ,可以枚举 。
总结一下:此时如果存在 ,或者 ,仍然令 为度数最大的点,删掉它然后直接判剩余的图是不是破碎的。否则只有 时 A 可能必胜,枚举 做同样的事情。
总结
对给定的图 ,
- 为空,A 必胜;
- 点数为偶且删去 中任意一个度数最大的点之后, 是破碎的,A 必胜;
- 为奇且 点数是不超过 的奇数的时候,若 , 删去 之后删去任意一个度数最大的点得到的图是破碎的,A 必胜;
- 否则,A 必败。
复杂度 ,认为 是常数。